2 Les algorithmes. Régularisation entropique

2.1 L’algorithme du simplexe

Le problème primal du transport optimal peut se réécrire sous cette forme : \[ \mathrm{L}_{\mathrm{\textbf{C}}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) = \underset{\substack{\mathrm{\textbf{p}}\in \mathbb{R}^{nm}_+\\ \mathbf{A}\mathrm{\textbf{p}}= \bigl[\begin{smallmatrix}\mathrm{\textbf{a}} \\ \mathrm{\textbf{b}}\end{smallmatrix} \bigr]}}{\min}\; \,{}^t{\mathrm{\textbf{c}}}\mathrm{\textbf{p}} \] où $p$ est l’énumération colonne par colonne de $\mathrm{\textbf{P}}$ et $\mathbf{A}= \begin{bmatrix} \,{}^t{\mathbb{1}_{n}} \otimes \mathbb{I}_m \\ \mathbb{I}_n \otimes \,{}^t{\mathbb{1}_{m}} \end{bmatrix}\in\mathcal{M}_{n+m,nm}(\mathbb{R})$ ($\otimes$ est le produit de Kronecker).

Ce problème, qui est un programme linéaire, est plus précisément appelé le problème du min-cost flow. Il existe des algorithmes efficaces pour le résoudre, y compris celui présenté dans cette section, le network-simplex. Avant de présenter l’algorithme, nous allons prouver quelques résultats intermédiaires qui seront très utiles pour expliquer son fonctionnement et sa correction.

Proposition 2.1 Supposons que $\mathrm{\textbf{P}}^\star$ soit solution du problème primal, et $(\mathrm{\textbf{f}}^\star, \mathrm{\textbf{g}}^\star)$ solution du problème dual. On a alors : \[\forall (i,j) \in[ 1,n ]\times[ 1,m ], \mathrm{\textbf{P}}^\star_{i,j}(\mathrm{\textbf{C}}_{i,j}-\mathrm{\textbf{f}}^\star_i+\mathrm{\textbf{g}}^\star_j)=0\]

Preuve. Par la dualité forte on a que : \[\begin{aligned} \langle \mathrm{\textbf{P}}^\star,\,\mathrm{\textbf{C}}\rangle &= \langle \mathrm{\textbf{f}}^\star,\,\mathrm{\textbf{a}}\rangle + \langle \mathrm{\textbf{g}}^\star,\,\mathrm{\textbf{b}}\rangle\\ &= \langle \mathrm{\textbf{f}}^\star,\,\mathrm{\textbf{P}}^\star\mathbb{1}_m\rangle+\langle \mathrm{\textbf{g}}^\star,\, \,{}^t{\mathrm{\textbf{P}}^\star}\mathbb{1}_n\rangle\\&= \langle \mathrm{\textbf{f}}^\star \,{}^t{\mathbb{1}_m},\,\mathrm{\textbf{P}}^\star\rangle+\langle \mathbb{1}_n \,{}^t{\mathrm{\textbf{g}}^\star},\,\mathrm{\textbf{P}}^\star\rangle\\ &= \langle \mathrm{\textbf{f}}^\star \,{}^t{\mathbb{1}_m}+\mathbb{1}_n \,{}^t{\mathrm{\textbf{g}}^\star},\,\mathrm{\textbf{P}}^\star\rangle \end{aligned}\] d’où : \[\langle \mathrm{\textbf{P}}^\star,\,\mathrm{\textbf{C}}- \mathrm{\textbf{f}}^\star\oplus \mathrm{\textbf{g}}^\star\rangle=0\] où l’on note $\mathrm{\textbf{f}}^\star\oplus\mathrm{\textbf{g}}^\star=(\mathrm{\textbf{f}}^\star_i+\mathrm{\textbf{g}}^\star_j)_{(i,j)\in[ 1,n ]\times[ 1,m ]}$.

Le résultat réciproque est également vrai et va particulièrement nous intéresser dans le cadre du network-simplex.

Définition 2.1 (Paire complémentaire) Une matrice $\mathrm{\textbf{P}}\in \mathcal{M}_n(\mathbb{R})$ et un couple $(\mathrm{\textbf{f}}, \mathrm{\textbf{g}})\in\mathbb{R}^n\times\mathbb{R}^m$ forment une paire complémentaire par rapport à $\mathrm{\textbf{C}}$ si, et seulement si, pour tout $(i, j)\in[ 1,n ]\times[ 1,m ]$ tel que $\mathrm{\textbf{P}}_{i,j}>0$, on a : $\mathrm{\textbf{C}}_{i,j} = \mathrm{\textbf{f}}_i + \mathrm{\textbf{g}}_j$.

Proposition 2.2 (Optimalité d’une paire complémentaire) Si $\mathrm{\textbf{P}}$ et $(\mathrm{\textbf{f}}, \mathrm{\textbf{g}})$ sont une paire complémentaire et respectivement des solution admissibles du problème primal et dual, alors elles sont des solutions optimales.

Preuve. Par la dualité faible, on a : \[\mathrm{L}_{\mathrm{\textbf{C}}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) \leq \langle \mathrm{\textbf{P}},\,\mathrm{\textbf{C}}\rangle = \langle \mathrm{\textbf{P}},\,\mathrm{\textbf{f}}\oplus \mathrm{\textbf{g}}\rangle = \langle \mathrm{\textbf{a}},\,\mathrm{\textbf{f}}\rangle + \langle \mathrm{\textbf{b}},\,\mathrm{\textbf{g}}\rangle \leq \mathrm{L}_{\mathrm{\textbf{C}}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})\] Et donc : \[\mathrm{L}_{\mathrm{\textbf{C}}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) = \langle \mathrm{\textbf{P}},\,\mathrm{\textbf{C}}\rangle = \langle \mathrm{\textbf{a}},\,\mathrm{\textbf{f}}\rangle + \langle \mathrm{\textbf{b}},\,\mathrm{\textbf{g}}\rangle\]

Un programme linéaire avec un ensemble de contraintes borné atteint sa solution optimale à un point extrémal du polyèdre convexe des solutions admissibles. Une manière de trouver une solution optimale est donc de visiter ces points particuliers de $\mathrm{\textbf{U}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})$, et de vérifier à chaque fois s’il s’agit d’une solution optimale. Nous allons montrer quelques propriétés sur les plans de transports associés aux points extrémaux de $\mathrm{\textbf{U}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})$.

Nous allons représenter notre problème sous la forme d’un graphe biparti. On considère $V = (1, 2, ..., n)$ et $V' = (1', 2', ..., m')$ deux ensembles de $n$ et $m$ sommets respectivement, et $E$ les $nm$ arêtes reliant chaque sommet de $V$ à $V'$. On définit alors $G = (V \cup V', E)$. A chaque arête $(i, j)$ on associe le coût $\mathrm{\textbf{C}}_{i,j}$. On peut donc reformuler le problème en un problème de flot sur le graphe G. Il s’agit de trouver un flot sur le graphe qui minimise le coup total des arêtes utilisées et qui vérifie deux propriétés :

le flot sortant du sommet $k$ est égal à $\mathrm{\textbf{a}}_k$;
le flot entrant dans un sommet $l'$ est égal à $\mathrm{\textbf{b}}_{l'}$.

On note $G(\mathrm{\textbf{P}})$ un graphe correspondant à un plan de transport $\mathrm{\textbf{P}}$ et où on n’a gardé que les arêtes de flot non nul. Formellement, $S(\mathrm{\textbf{P}}) = \{(i,j)\in E, \mathrm{\textbf{P}}_{i,j}>0 \}$ et $G(\mathrm{\textbf{P}}) = (V \cup V', S(\mathrm{\textbf{P}}))$.

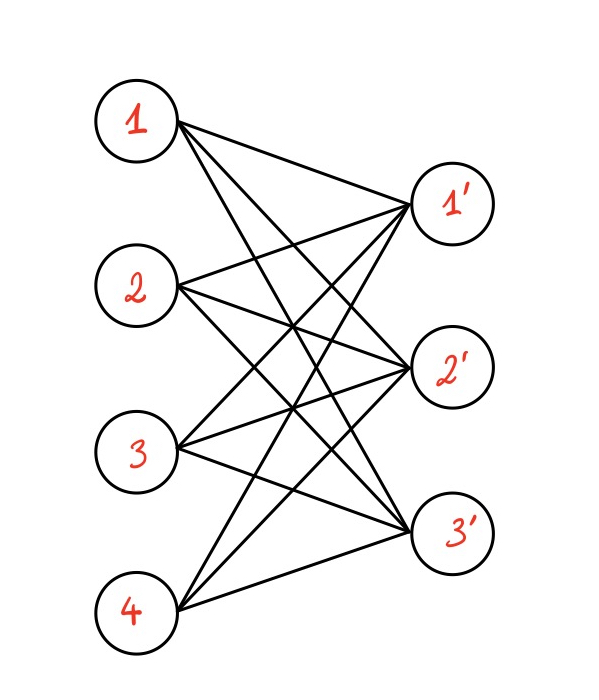
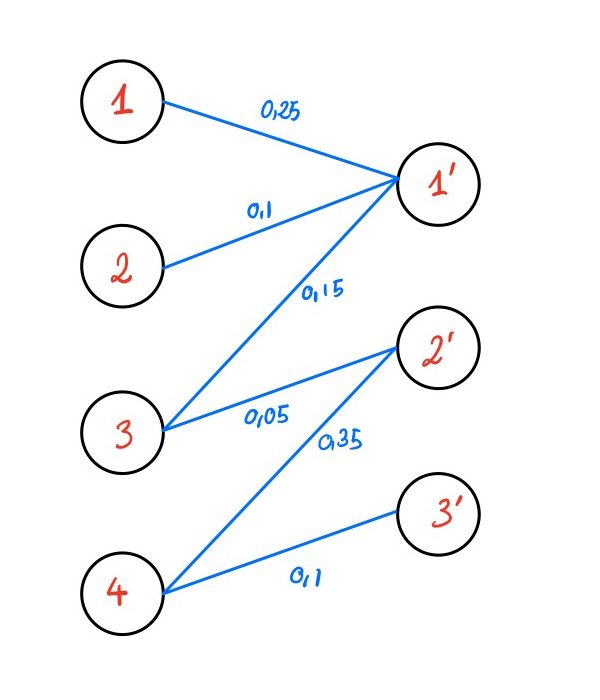
Figure 2.1: Exemple du graphe $G$ pour $\mathbf{a} = [0.35,0.2,0.45]$ et $\mathbf{b} = [0.5,0.4,0.1]$ et d’un plan de transport admissible.

Proposition 2.3 Soit $\mathrm{\textbf{P}}$ un point extrémal de $\mathrm{\textbf{U}}(\mathrm{\textbf{a}}, \mathrm{\textbf{b}})$. Alors $G(\mathrm{\textbf{P}})$ est sans cycle et en particulier $\mathrm{\textbf{P}}$ a au plus $n + m -1$ entrées non nulles.

Preuve. On suppose que $\mathrm{\textbf{P}}$ est un point extrémal de $\mathrm{\textbf{U}}(\mathrm{\textbf{a}}, \mathrm{\textbf{b}})$ et que $G(\mathrm{\textbf{P}}) =(V \cup V', S(\mathrm{\textbf{P}}))$ possède un cycle et on va montrer le résultat par l’absurde. On suppose donc qu’il existe $i_1,...,i_k \in [ 1,n ]$ et $j_i,...,j_k \in [ 1,m ]$ tels que : \[H = \{(i_1, j'_1), (j'_1, i_2), (i_2, j'_2), ..., (j'_k, i_1)\} \subset S(\mathrm{\textbf{P}})\] (Notez que le graphe $G$ n’est pas dirigé et que les arêtes sont écrites de cette manière pour faciliter la lecture de la preuve). On va maintenant construire $\mathrm{\textbf{Q}}$ et $\mathrm{\textbf{R}}$ tels que $P = \frac{\mathrm{\textbf{Q}}+ \mathrm{\textbf{R}}}{2}$, et $\mathrm{\textbf{Q}}, \mathrm{\textbf{R}}\neq \mathrm{\textbf{P}}$. Si on réussit une telle construction cela voudra dire que $\mathrm{\textbf{P}}$ n’est pas un point extrémal de $\mathrm{\textbf{U}}(\mathrm{\textbf{a}}, \mathrm{\textbf{b}})$ et cela conclura notre preuve par l’absurde.
On pose $\varepsilon < \underset{(i, j)\in S(\mathrm{\textbf{P}})}{\min}\;\mathrm{\textbf{P}}_{i,j}$, et $\mathbf{E}$ une matrice telle que : \[\mathbf{E}_{i,j} = \begin{cases} \varepsilon &\text{ si } (i, j') \in H \\ -\varepsilon &\text{ si } (j', i) \in H \\ 0 &\text{ sinon } \end{cases}\] On pose maintenant $\mathrm{\textbf{Q}}= \mathrm{\textbf{P}}+ \mathbf{E}$ et $\mathrm{\textbf{R}}= \mathrm{\textbf{P}}- \mathbf{E}$. On a choisi $\varepsilon$ suffisamment petit pour que $\mathrm{\textbf{R}}$ n’ait pas d’élément négatif. Par construction, chaque colonne (respectivement ligne) de $\mathbf{E}$ comporte soit uniquement des zéros, soit un unique indice de valeur $\varepsilon$ et un unique indice de valeur $-\varepsilon$. On a donc $\mathbf{E}\mathbb{1}_{m}=\mathbb{0}_{n}$ et $\,{}^t{\mathbf{E}}\mathbb{1}_{n}=\mathbb{0}_{m}$, et donc $\mathrm{\textbf{Q}}$ et $\mathrm{\textbf{R}}$ sont des solutions admissibles.

Remarque 2.1. Comme $G(\mathrm{\textbf{P}})$ est sans cycle, c’est soit un arbre, c’est-à-dire un graphe sans cycle connexe, soit une forêt, c’est à dire une union d’arbres.

L’idée générale de l’algorithme est assez classique. On sélectionne un point extrémal arbitraire de $\mathrm{\textbf{U}}(\mathrm{\textbf{a}}, \mathrm{\textbf{b}})$. Si c’est une solution optimale, on s’arrête. Sinon on sélectionne un autre point extrémal de manière à ce qu’il ait un coût plus faible. On continue l’opération jusqu’à tomber sur une solution optimale. Nous allons montrer pas-à-pas que cet algorithme est en effet implémentable.

2.1.1 Sélectionner un point de départ pour notre algorithme

Une manière d’obtenir un point extrémal de $\mathrm{\textbf{U}}(\mathrm{\textbf{a}}, \mathrm{\textbf{b}})$ est d’utiliser la méthode du Nord-Ouest, qui permet d’obtenir un tel point en $n + m$ opérations. Nous la décrivons dans ce paragraphe.

\begin{algorithm} \caption{Règle du Nord-Ouest} \begin{algorithmic} \Procedure{NorthWest}{$\mathbf{a}_1, \mathbf{b}_1$} \State $i \gets 1$ \State $j \gets 1$ \State $r \gets \mathbf{a}_1$ \State $c \gets \mathbf{b}_1$ \While{ $i \leq n$ et $j \leq m$} \State $t \gets \min(r, c)$ \State $\mathbf{P}_{i,j} \gets t$ \State $r \gets r - t$ \State $c \gets s- t$ \If{$r = 0$} \State $i \gets i + 1$ \State $r \gets \mathbf{a}_i$ \EndIf \If{$c = 0$} \State $j \gets j + 1$ \State $c \gets \mathbf{b}_j$ \EndIf \EndWhile \EndProcedure \end{algorithmic} \end{algorithm}

Exemple 2.1 Pour $\mathrm{\textbf{a}}=[0.4,0.3,0.3]$ et $\mathrm{\textbf{b}}=[0.5,0.2,0.3]$: \[\begin{aligned}\begin{bmatrix} \bullet & 0 & 0 \\ 0 & 0 & 0 \\ 0& 0 & 0\end{bmatrix} &\rightarrow \begin{bmatrix} 0.4 & 0 & 0 \\ \bullet & 0 & 0 \\ 0& 0 & 0\end{bmatrix} &\rightarrow \begin{bmatrix} 0.4 & 0 & 0 \\ 0.1 & \bullet & 0 \\ 0& 0 & 0\end{bmatrix}\\ &\rightarrow \begin{bmatrix} 0.4 & 0 & 0 \\ 0.1 &0.2 &0 \\ 0& 0 &\bullet \end{bmatrix} & \rightarrow \begin{bmatrix} 0.4 & 0 & 0 \\ 0.1 &0.2 &0 \\ 0& 0 & 0.3\end{bmatrix}\end{aligned}\]

2.1.2 Vérifier qu’une solution est ou non optimale

On a montré à la Proposition 2.2 une méthode pour vérifier si une solution $\mathrm{\textbf{P}}$ est ou non optimale. Il suffit de prendre sa paire duale $(\mathrm{\textbf{f}}, \mathrm{\textbf{g}})$ et de vérifier s’il s’agit d’un couple admissible du problème dual.

Étant donné un plan de transport admissible $\mathrm{\textbf{P}}$, on peut trouver un paire complémentaire en résolvant : \[\forall\,(i, j)\in[ 1,n ]\times[ 1,m ], \mathrm{\textbf{f}}_i +\mathrm{\textbf{g}}_j = \mathrm{\textbf{C}}_{i,j}\]

2.1.3 Mise à jour du réseau

Si la solution $\mathrm{\textbf{P}}$ n’est pas optimale, c’est qu’il existe $(i, j)$ tel que $\mathrm{\textbf{f}}_i + \mathrm{\textbf{g}}_j < \mathrm{\textbf{C}}_{i,j}$.

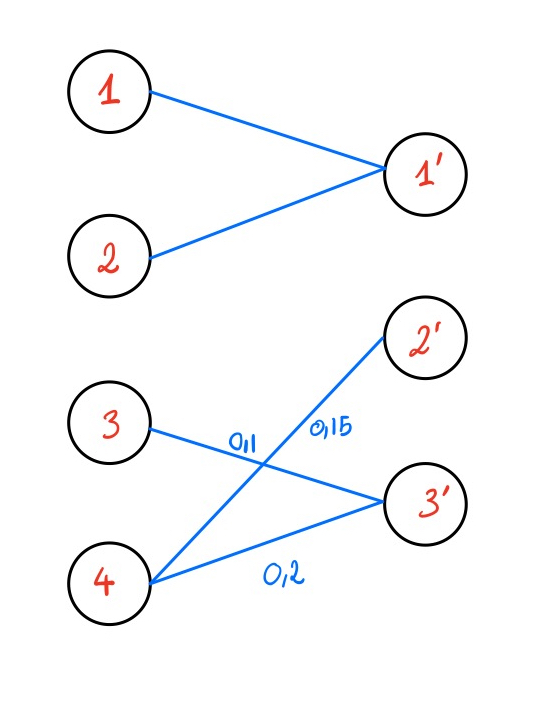
On ajoute alors au graphe $G(\mathrm{\textbf{P}})$ l’arête $(i, j)$. Deux cas de figures peuvent alors se présenter :

L’arête $(i ,j)$ relie deux sous-arbres de la forêt $G(\mathrm{\textbf{P}})$. $G(\mathrm{\textbf{P}})$ est donc toujours une forêt, et donc $\mathrm{\textbf{P}}$ ne change pas. On peut utiliser la procédure de la Section 2.1.2 pour calculer à nouveau la paire complémentaire $(\mathrm{\textbf{f}}, \mathrm{\textbf{g}})$.
Le graphe $G(\mathrm{\textbf{P}})$ a maintenant un cycle, que l’on note : \[\{(i_1, j'_1), (j'_1, i_2), ..., (j'_l, i_1) \} \text{ où } (i_1, j'_1) = (1, j)\] On appelle arêtes positives (respectivement négatives) les arêtes de ce cycle de la forme $(i_k, j'_k)$ (respectivement $(j'_k, i_{k+1})$). On définit $\varepsilon$ comme étant le flot minimal des arêtes négatives du cycle. Par la suite, on diminue le flot de toutes les arêtes négatives du cycle de $\varepsilon$, et on augmente de la même quantité les autres arêtes du cycle. Cela permet d’enlever l’arête négative de flot minimal et de rompre le cycle. On obtient alors la solution mise à jour $\tilde{\mathrm{\textbf{P}}}$ et on peut calculer la nouvelle paire duale complémentaire $(\mathrm{\textbf{f}},\mathrm{\textbf{g}})$.

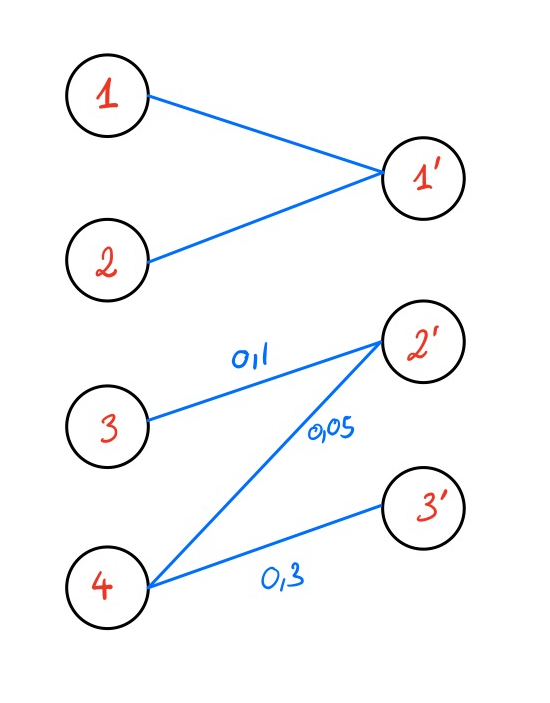
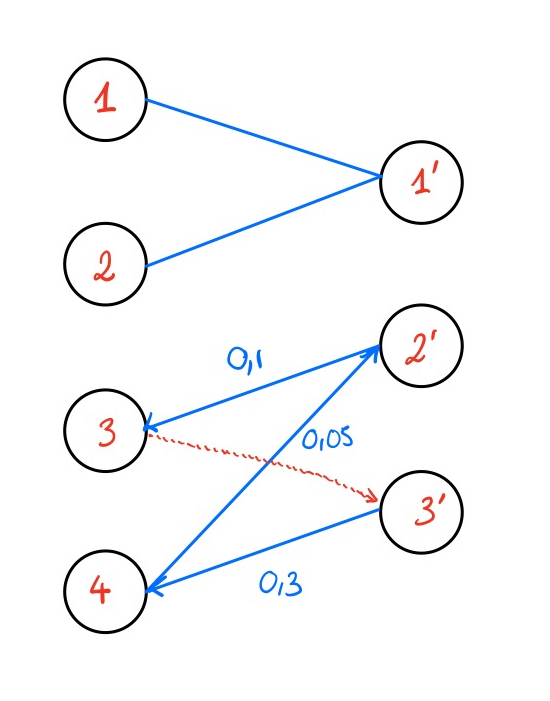
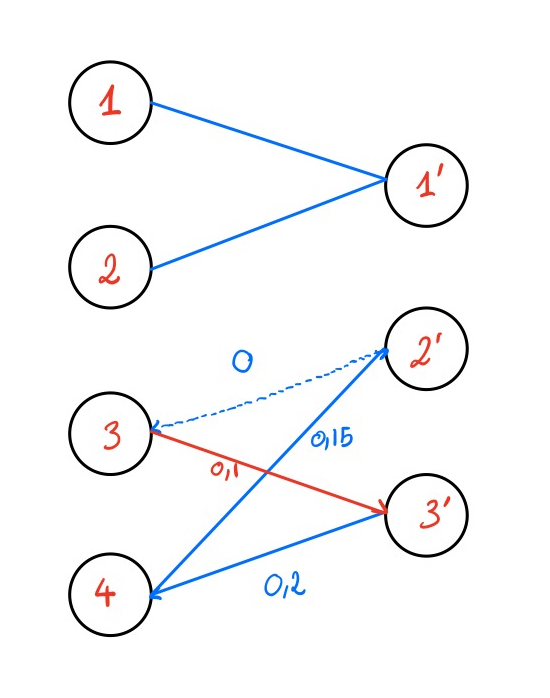
$G(\mathbf{P})$ avant la mise à jour du réseau

Théorème 2.1 La procédure décrite dans la Section 2.1.3 améliore le coût de la solution $\mathrm{\textbf{P}}$. C’est-à-dire que si $\mathrm{\textbf{P}}$ est mis à jour en $\tilde{\mathrm{\textbf{P}}}$, on a $\langle \mathrm{\textbf{P}},\,\mathrm{\textbf{C}}\rangle \geq \langle \tilde{\mathrm{\textbf{P}}},\mathrm{\textbf{C}}\rangle$.

Preuve. Le cas intéressant ici est de voir ce qu’il se passe lorsque qu’un cycle est créé au cours de la mise à jour du network-simplex. Dans ce cas, $\mathrm{\textbf{P}}$ est mis à jour en $\tilde{\mathrm{\textbf{P}}}$ et on a cette équation : \[\langle \tilde{\mathrm{\textbf{P}}},\,\mathrm{\textbf{C}}\rangle-\langle \mathrm{\textbf{P}},\,\mathrm{\textbf{C}}\rangle= \varepsilon \left(\;\sum_{k=1}^{l} \mathrm{\textbf{C}}_{i_k,j_k} - \sum_{k=1}^{l}\mathrm{\textbf{C}}_{i_{k+1},j_k}\right)\] Cela correspond à l’augmentation de coût correspondant aux arêtes où on a rajouté $\varepsilon$ aux poids moins la diminution correspondant aux arêtes négatives où on a enlevé $\varepsilon$ aux poids. Soit $(\mathrm{\textbf{f}}, \mathrm{\textbf{g}})$ la paire complémentaire associée à $\mathrm{\textbf{P}}$. Elle vérifie \[\forall\,(v, w), \mathrm{\textbf{f}}_v + \mathrm{\textbf{g}}_w = C_{vw}\] Donc on peut réécrire : \[\begin{aligned}\sum_{k=1}^{l} \mathrm{\textbf{C}}_{i_k,j_k} - \sum_{k=1}^{l}\mathrm{\textbf{C}}_{i_{k+1},j_k} &= \mathrm{\textbf{C}}_{i,j} + \sum_{k=2}^{l} \mathrm{\textbf{f}}_{i_k}+\mathrm{\textbf{g}}_{j_k} - \sum_{k=1}^{l} \mathrm{\textbf{f}}_{i_{k+1}}+\mathrm{\textbf{g}}_{j_k}\\ &= \mathrm{\textbf{C}}_{i,j} - (\mathrm{\textbf{f}}_{i} +\mathrm{\textbf{g}}_{j}). \end{aligned}\] Ce dernier terme est négatif car $i$ et $j$ ont été choisis car $\mathrm{\textbf{f}}_i + \mathrm{\textbf{g}}_j < \mathrm{\textbf{C}}_{i,j}$, ce qui prouve le résultat.

Finalement l’algorithme du network-simplex peut être résumé ainsi :

\begin{algorithm} \caption{Network-Simplex} \begin{algorithmic} \Procedure{NetworkSimplex}{$\mathbf{a}, \mathbf{b}$} \State $\mathbf{P} \gets$ \Call{NorthWest}{$\mathbf{a}, \mathbf{b}$} \State $G \gets G(\mathbf{P})$ \State $(\mathbf{f}, \mathbf{g}) \gets$ \Call{PaireComplémentaire}{$\mathbf{P}$} \While{$\mathbf{P}$ et $(\mathbf{f}, \mathbf{g})$ ne sont pas des solutions admissibles} \State \Call{MiseÀJour}{} \EndWhile \EndProcedure \end{algorithmic} \end{algorithm}

Il a été prouvé par Tarjan (1997) que cet algorithme a une complexité polynomiale et plus particulièrement une complexité de : \[O\left(\,(n+m)nm\log(n+m)\log\left((n+m)\|\mathrm{\textbf{C}}\|_\infty\right)\,\right)\] En pratique, cet algorithme est très efficace.

2.2 Régularisation entropique, Sinkhorn

Bien que l’algorithme décrit dans la section précédente soit très efficace en pratique, lorsque la dimension de $\mathrm{\textbf{a}}$ et $\mathrm{\textbf{b}}$ dépasse quelques centaines, le coût d’exécution du network-simplex devient prohibitif. C’est ce qui a retardé pendant longtemps l’utilisation du transport optimal dans des contextes d’apprentissage avec des données assez larges. Cependant, en 2013, Cuturi (2013) propose une régularisation du problème du transport optimal qui permet d’approximer un plan de transport optimal très rapidement.

2.2.1 Régularisation entropique

Définition 2.8. On définit l’entropie discrète d’une matrice de couplage $\mathrm{\textbf{P}}$ par : \[\mathrm{\textbf{H}}(\mathrm{\textbf{P}}) \stackrel{\text{déf.}}= -\sum_{i,j} \mathrm{\textbf{P}}_{i,j} (\log(\mathrm{\textbf{P}}_{i,j})-1)\]

On va maintenant pouvoir définir le problème du transport optimal régularisé.

Définition 2.2 Le problème du transport optimal régularisé correspond à résoudre : \[\mathrm{L}_\mathrm{\textbf{C}}^\varepsilon(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) \stackrel{\text{déf.}}= \underset{\mathrm{\textbf{P}}\in \mathrm{\textbf{U}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})}{\min}\; \langle \mathrm{\textbf{P}},\,\mathrm{\textbf{C}}\rangle - \varepsilon \mathrm{\textbf{H}}(\mathrm{\textbf{P}}) \tag{2.1}\]

Le terme $\mathrm{\textbf{H}}(\mathrm{\textbf{P}})$ est donc utilisé ici comme un terme de régularisation pour obtenir des solutions approchées du problème du transport optimal.

Remarque 2.2. On peut vérifier qu’on a en particulier :

$\mathrm{L}_\mathrm{\textbf{C}}^\varepsilon(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) \overset{\varepsilon \rightarrow 0}{\longrightarrow} \mathrm{L}_\mathrm{\textbf{C}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})$
$\mathrm{\textbf{P}}_\varepsilon \overset{\varepsilon \rightarrow \infty}{\longrightarrow} \mathrm{\textbf{a}}\otimes \mathrm{\textbf{b}}= \mathrm{\textbf{a}} \,{}^t{\mathrm{\textbf{b}}} = (\mathrm{\textbf{a}}_i \, \mathrm{\textbf{b}}_j)_{(i,j)\in[ 1,n ]\times[ 1,m ]}$

On s’aperçoit également empiriquement que les solutions associées au problème régularisé sont plus diffuses, comme on peut le voir avec la Figure 2.3.

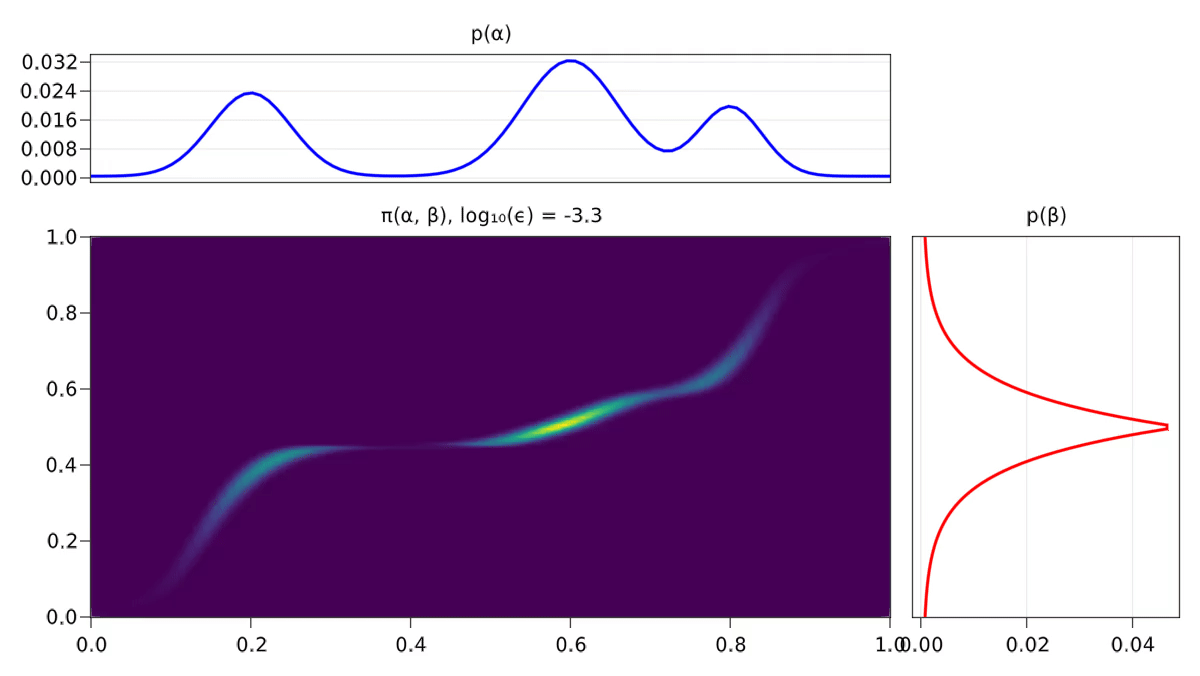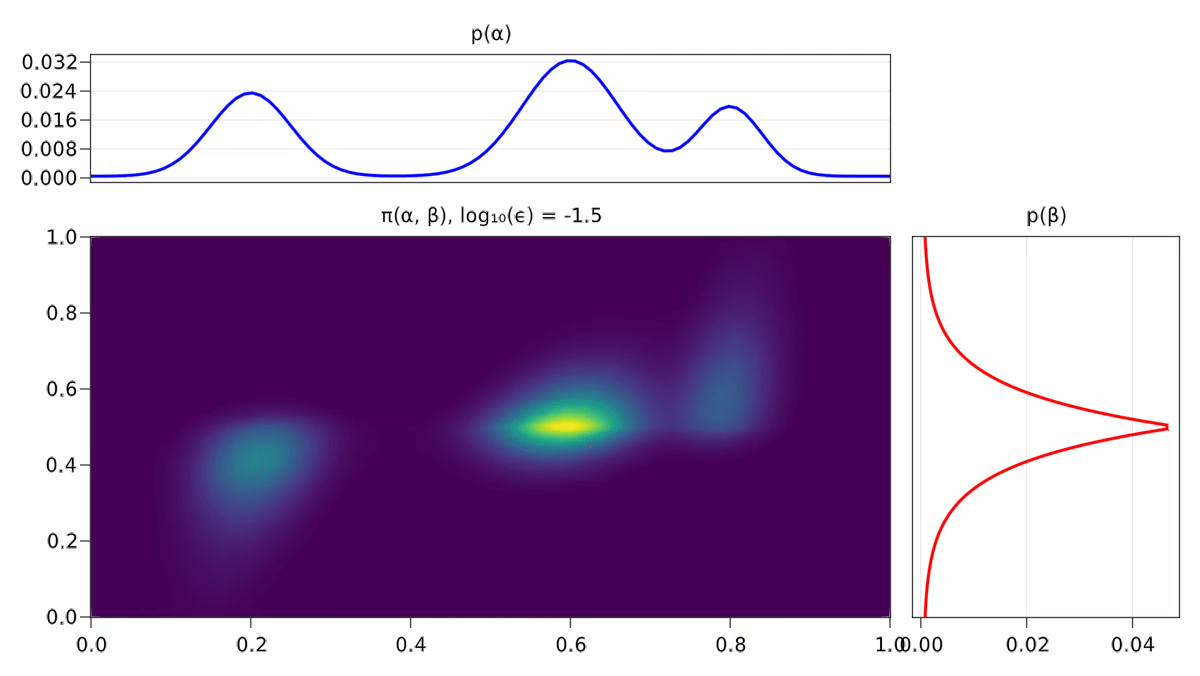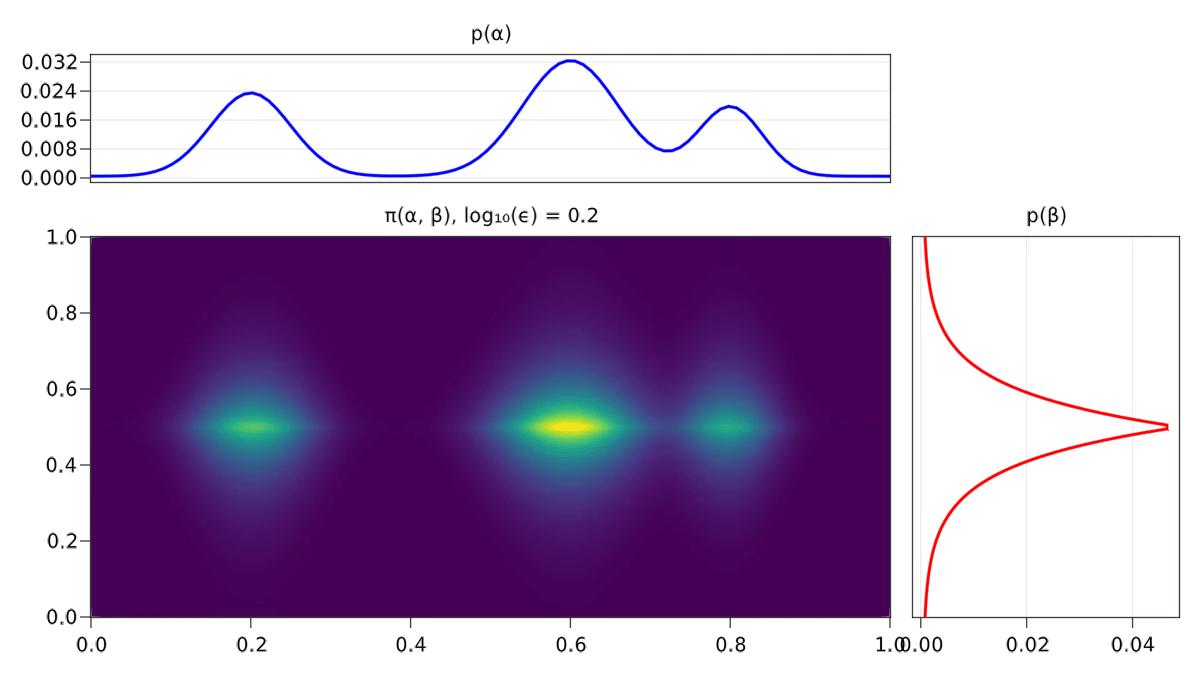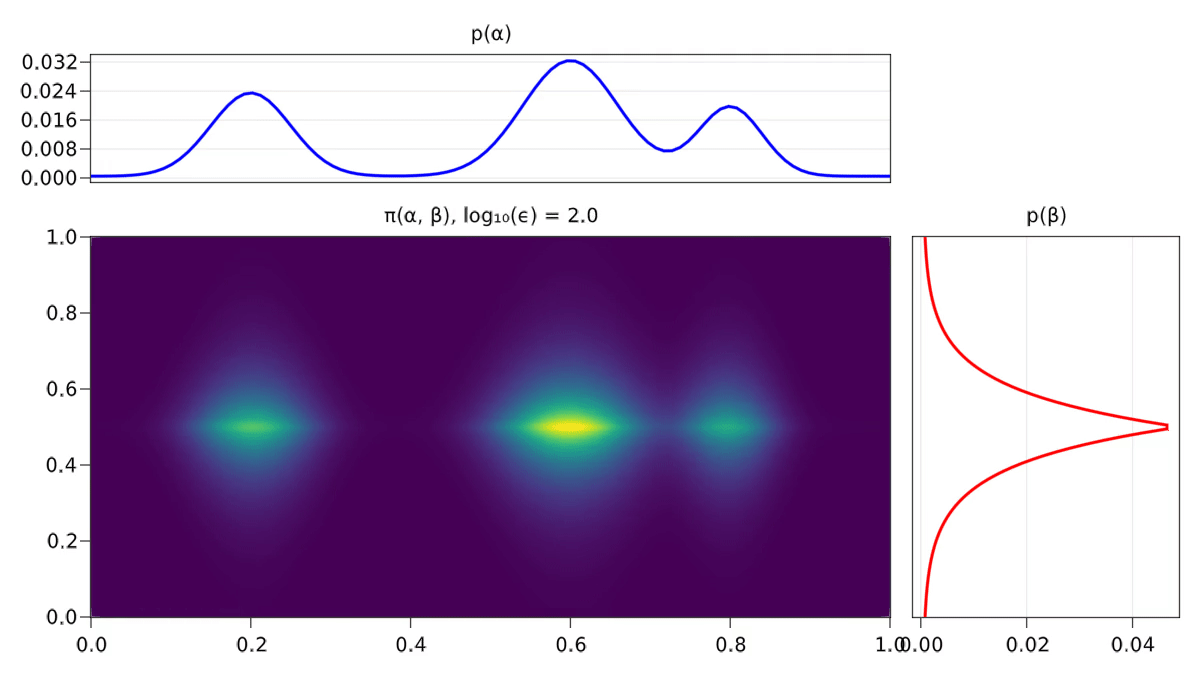
Figure 2.3: Exemple de solutions du problème régularisé pour différentes valeurs de $\varepsilon$.

2.2.2 Algorithme de Sinkhorn

Proposition 2.4 La solution au transport optimal régularisé a la forme : \[\forall \,(i,j) \in [ 1,n ] \times [ 1,m ], \quad \mathrm{\textbf{P}}_{i,j} = \mathrm{\textbf{u}}_i \mathrm{\textbf{K}}_{i,j} \mathrm{\textbf{v}}_j\] où K est le kernel de Gibbs, $\mathrm{\textbf{K}}_{i,j} \stackrel{\text{déf.}}= \exp\left({-\frac{\mathrm{\textbf{C}}_{i,j}}{\varepsilon}}\right)$, et où $\mathrm{\textbf{u}}$ et $\mathrm{\textbf{v}}$ sont des inconnues.

Preuve. On écrit le lagrangien $\Lambda_{\mathrm{\textbf{C}}}^{\varepsilon}$ associé au problème $\mathrm{L}_\mathrm{\textbf{C}}^\varepsilon(\mathrm{\textbf{a}},\mathrm{\textbf{b}})$ \[\Lambda_{\mathrm{\textbf{C}}}^{\varepsilon}(\mathrm{\textbf{P}}, \mathrm{\textbf{f}}, \mathrm{\textbf{g}}) = \langle \mathrm{\textbf{P}},\,\mathrm{\textbf{C}}\rangle - \varepsilon \mathrm{\textbf{H}}(\mathrm{\textbf{P}}) - \langle \mathrm{\textbf{f}},\,\mathrm{\textbf{P}}\mathbb{1}_m-\mathrm{\textbf{a}}\rangle-\langle \mathrm{\textbf{g}},\, \,{}^t{\mathrm{\textbf{P}}}\mathbb{1}_n-\mathrm{\textbf{b}}\rangle\] Lorsque le minimum est atteint la dérivée s’annule et on a donc : \[\frac{\partial\mathcal{E}(\mathrm{\textbf{P}},\mathrm{\textbf{f}},\mathrm{\textbf{g}})}{\partial \mathrm{\textbf{P}}_{i,j}}= \mathrm{\textbf{C}}_{i,j} + \varepsilon \log(\mathrm{\textbf{P}}_{i,j}) - \mathrm{\textbf{f}}_i -\mathrm{\textbf{g}}_j=0\] D’où, si $P$ est une solution optimale on a $\mathrm{\textbf{P}}_{i,j}=e^{\mathrm{\textbf{f}}_i/\varepsilon}e^{-\mathrm{\textbf{C}}_{i,j}/\varepsilon}e^{\mathrm{\textbf{g}}_j/\varepsilon}$ ce qui correspond à l’expression recherchée.

On peut donc réécrire le transport optimal régularisé sous forme matricielle ainsi :

\[\mathrm{\textbf{P}}=\mathop{\mathrm{diag}}(\mathrm{\textbf{u}})\mathrm{\textbf{K}}\mathop{\mathrm{diag}}(\mathrm{\textbf{v}})\] avec les conditions sur $\mathrm{\textbf{u}}$ et $\mathrm{\textbf{v}}$ suivantes et dues à la conservation de la masse :

$\mathrm{\textbf{u}}\odot (\mathrm{\textbf{K}}\mathrm{\textbf{v}}) = \mathrm{\textbf{a}} \quad \text{et} \quad \mathrm{\textbf{v}}\odot ( \,{}^t{\mathrm{\textbf{K}}}\mathrm{\textbf{u}}) = \mathrm{\textbf{b}}$ et où $\odot$ correspond à la multiplication vectorielle terme à terme.

Il se trouve que le problème défini par l’Équation 2.1 réécrit sous cette forme est une instance d’un problème numérique bien connu appelé matrix scaling et dont il existe un algorithme efficace que nous allons décrire ci-dessous.

\begin{algorithm} \caption{Algorithme de Sinkhorn} \begin{algorithmic} \Procedure{Sinkhorn}{$\mathbf{a}, \mathbf{b}$} \State $\mathbf{u} \gets \mathbb{1}_n$ \State $\mathbf{v} \gets \mathbb{1}_m$ \State $\mathbf{P} \gets \operatorname{diag} (\mathbf{u}) \mathbf{K} \operatorname{diag} (\mathbf{v})$ \While{$\mathbf{P}$ change} \State $\mathbf{u} \gets \frac{\mathbf{a}}{\mathbf{K} \mathbf{v}}$ \State $\mathbf{v} \gets \frac{\mathbf{b}}{{}^t\mathbf{K} \mathbf{u}}$ \State $\mathbf{P} \gets \operatorname{diag} (\mathbf{u}) \mathbf{K} \operatorname{diag} (\mathbf{v})$ \EndWhile \EndProcedure \end{algorithmic} \end{algorithm}

Il est prouvé par Cuturi (2013) que la complexité de cet algorithme est en $O(n^3 log(n))$ avec une complexité empirique en $O(n^2)$. L’algorithme du Sinkhorn calculant essentiellement des multiplications matricielles est également très parallélisable (pour par exemple calculer plusieurs solutions au problème défini par l’Équation 2.1 en même temps) et peut notamment être exécuté sur GPU, ce qui rend cet algorithme bien plus efficace dans des contextes d’apprentissage, où il y a beaucoup de données à traiter.

La convergence de l’algorithme de Sinkhorn est assurée comme il a été montré par Franklin et Lorenz (1989).