4 Applications en apprentissage statistique
Nous allons présenter deux applications différentes du transport optimal en apprentissage, qui ont émergé de la recherche ces dernières années, conséquence de l’apparition des nouvelles méthodes pour approximer une solution au problème du transport grâce notamment à l’algorithme du Sinkhorn.
4.1 Les réseaux antagonistes génératifs (GAN)
Contrairement à la plupart des modèles utilisés en apprentissage statistique qui sont souvent des modèles prédictifs, les réseaux antagonistes génératifs sont des modèles génératifs qui appartiennent à la catégorie de l’apprentissage non supervisé. À partir d’un grand nombre d’exemples issus d’une distribution inconnue, le GAN apprend à générer de nouveau exemples qui suivent la même distribution. Ces méthodes ont produits des résultats stupéfiants ces dernières années comme on peut le voir sur la Figure 4.1.



4.1.1 Fonctionnement des GAN
Les GAN s’appuient sur une structure particulière composée d’un générateur et d’un discriminateur. Le générateur a la tâche de générer des exemples indicernables des exemples provenant des données réelles, tandis que le discriminateur tente de différencier les exemples réels des exemples générés. L’entraînement est une compétition entre le générateur, qui essaie de tromper le discriminateur, et le discriminateur qui tente de ne pas être trompé.
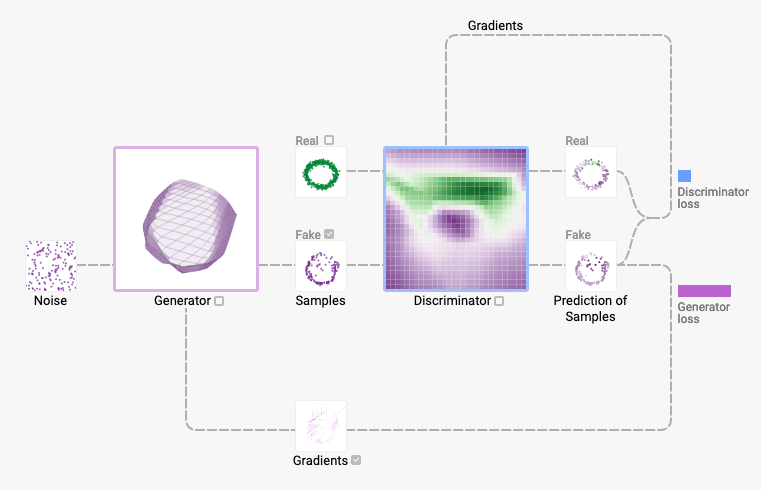
Rentrons un peu plus dans les détails. On note \(\mu\in\mathop{\mathrm{P}}(\mathcal{X})\) la distribution des données réelles et que l’on cherche à estimer. On définit une variable aléatoire avec une distribution fixe \(\rho\), dont on passe des réalisations par une fonction \(g_\theta : \mathcal{Z}\rightarrow \mathcal{X}\) qui génère des exemples suivant une certaine distribution \(\mu_\theta\in\mathop{\mathrm{P}}(\mathcal{X})\). La fonction \(g\) peut par exemple être un réseau neuronal paramétré par \(\theta\).
L’idée est de pouvoir mesurer la proximité entre les distributions \(\mu\) et \(\mu_\theta\). On cherche donc à définir une distance ou une divergence \(l(\mu_\theta, \mu)\). Un des critères d’importance est l’impact de cette divergence ou cette distance sur la convergence des suites de distribution de probabilité.
On dit qu’une suite \(\mu_n\) converge vers \(\mu\) si, et seulement si, \(l(\mu_n, \mu)\rightarrow 0\), et donc la notion de convergence associée dépend de \(l\). Pour optimiser notre modèle et donc optimiser le paramètre \(\theta\), il est souhaitable que l’application \(\theta \rightarrow \mu_\theta\) soit continue, et donc que lorsque \(\theta_n \rightarrow \theta, \mu_{\theta_n} \rightarrow \mu_\theta\). La distance ou divergence \(l\) doit donc préférablement induire une convergence la plus faible possible, qui garde du sens, afin qu’un grand nombre de suites convergent et qu’on puisse utiliser \(l(\mu_\theta, \mu)\) comme une fonction de coût.
4.1.2 Apport du transport optimal
La réponse à la discussion commencée à la Section 4.1.1 apportée par les GAN est d’utiliser une divergence telle que la divergence de Kullback-Leibler ou celle de Jensen-Shannon qui ont été définies au Chapitre 3.
Arjovsky, Chintala, et Bottou (2017) apportent une amélioration conséquente aux GAN (désormais WGAN) en proposant d’utiliser à la place des divergences mentionnées plus haut une distance de Wasserstein. Comme discuté au Chapitre 3 (Théorème 3.1) cette distance est plus naturelle que les divergences de Kullback-Leibler ou de Jensen-Shannon, elle induit une convergence plus faible (précisément la convergence en loi, ou convergence étroite) sur l’espace des distributions et permet également de beaucoup mieux comparer des distributions de supports différents.
Arjovsky, Chintala, et Bottou (2017) ont également constaté des améliorations empiriques dans l’entraînement du GAN, telles qu’une meilleure stabilité, et une métrique qui a plus de sens et qui est mieux corrélée avec la qualité des exemples.
Nous montrons ci-après les résultats que nous avons obtenu en utilisant un WGAN sur l’ensemble de données MNIST, qui correspond à des chiffres manuscrits.


4.2 Adaptation de domaine
4.2.1 Motivation du problème de l’adaptation de domaine
Il arrive souvent en apprentissage statistique que les données réelles ne soient pas distribuées tout à fait de la même manière que les données étiquetées utilisées pour l’entraînement du modèle. Par exemple en vision par ordinateur, cela peut être dû à une différence d’éclairage entre les données d’entraînement et réelles, ou alors une différence avec l’appareil d’acquisition ou encore la présence ou l’absence d’un fond. On peut facilement imaginer que ce genre de différences peut survenir dans d’autres contextes en apprentissage statistique. Le problème de l’adaptation de domaine est celui, à l’aide d’un modèle entraîné, d’obtenir les meilleures performances possibles sur les données réelles. Ces dernières années plusieurs équipes de recherches ont proposés des avancées encourageantes en utilisant le transport optimal.

4.2.2 Formalisation du problème
Soit \(\Omega \subset \mathbb{R}^d\) l’espace des entrées et \(\mathcal{C}\) l’espace des étiquettes. On note \(\mathop{\mathrm{P}}(\Omega)\) l’ensemble des mesures de probabilités sur \(\Omega\). Le paradigme d’apprentissage classique suppose l’existence d’un ensemble d’exemples étiquetés \(\{(x_{train}, y_{train})\in\Omega\times\mathcal{C}\}\) qui suivent la distribution jointe \(\pi\), et d’un ensemble d’exemples \(\{x_{test}\in\Omega\}\) dont on ne connaît pas (et on souhaite déterminer) les étiquettes. Pour déterminer les étiquettes des \(x_{test}\) on utilise souvent une estimation empirique de \(\pi\) et on fait l’hypothèse que \(x_{train}\) et \(x_{test}\) suivent la même distribution.
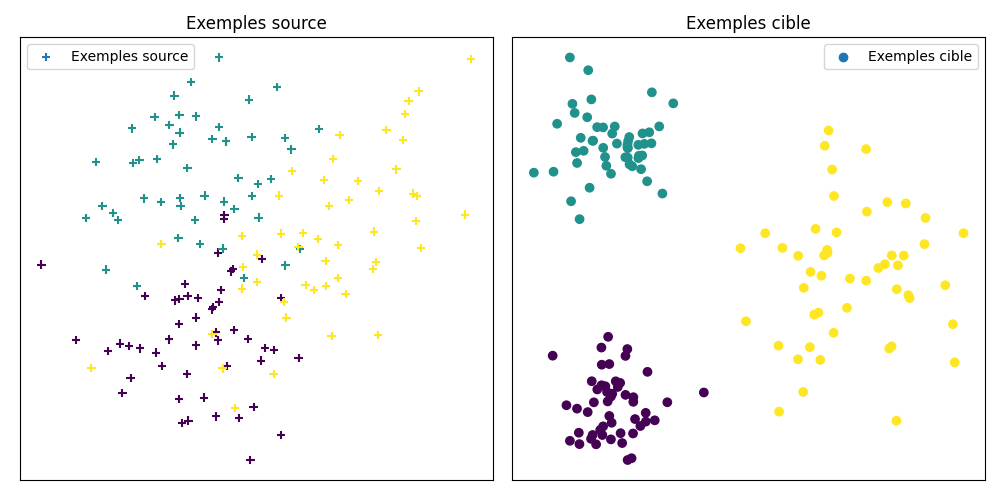
Le problème de l’adaptation de domaine ne fait pas cette dernière hypothèse et suppose au contraire l’existence de deux distributions jointes \(\pi_s\) et \(\pi_c\) relatives respectivement à un domaine source \(\Omega_s\) et un domaine cible \(\Omega_c\). On note \(\mu_s\), \(\mu_c\) les marginales respectives sur \(\mathcal{X}\).
On suppose également que la différence de distribution des exemples dans le domaine source et cible provient d’une transformation \(T : \Omega_s \rightarrow \Omega_c\) de l’espace des exemples. Finalement, on fait l’hypothèse que \(T\) préserve les distribution conditionnelles, c’est à dire que : \[\pi_s(y\mid x^s) = \pi_c(y\mid T(x^s))\]
4.2.3 Apport du transport optimal
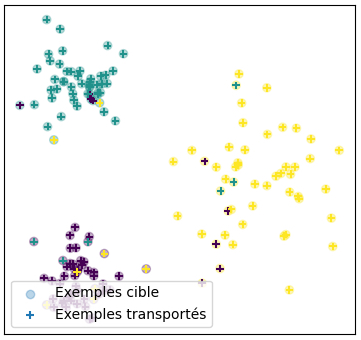
L’approche suggérée par Courty et al. (2016) est alors de chercher une application \(T\) qui transporte \(\mu_s\) sur \(\mu_c\) avec un coût minimal, le coût étant ici la distance euclidienne. Une fois ce plan de transport \(T\) calculé par les méthodes numériques exposées plus haut, on peut transporter les exemples sources dans l’espace cible \(\Omega_c\) et ainsi entraîner un modèle directement dans l’espace cible. Nous présentons à la Figure 4.4 les résultats d’expériences sur l’adaptation de domaine que nous avons menés sur un ensemble de données très simple. Les résultats très intéressants présentés par Courty et al. (2016) ont été suivis d’autres publications exploitant des idées similaires notamment (Courty et al. 2017), (Damodaran et al. 2018) et l’utilisation des distances de Gromov-Wasserstein pour l’adaptation de domaines hétérogènes plus récemment (Vayer et al. 2020).