1 Le problème du transport optimal
1.1 Le problème selon Kantorovitch
1.1.1 Formulation générale
Soit \(\mathcal{X}\) et \(\mathcal{Y}\) deux espaces mesurables, et \(\mu\in\mathop{\mathrm{P}}(\mathcal{X})\), \(\nu\in\mathop{\mathrm{P}}(\mathcal{Y})\) deux mesures de probabilité sur \(\mathcal{X}\) et \(\mathcal{Y}\) respectivement.
Remarque 1.1. L’hypothèse importante est que les mesures soient de même masse totale finie (conservation de la masse lors du transport).
Le problème de Monge-Kantorovitch est une version relaxée et symétrisée par Kantorovitch du problème du transport optimal de Monge (dans le sens où l’on peut fractionner la masse d’un point de la distribution initiale). Il se formule de la manière suivante :
Définition 1.1 (Problème de Monge-Kantorovitch) \[ \mathcal{L}_c(\mu,\nu) \stackrel{\text{déf.}}= \underset{\pi \in \mathit{\Pi}(\mu,\nu)}{\inf} \int_{\mathcal{X}\times \mathcal{Y}} c(x,y) \, \mathrm d \pi(x,y) = \underset{\pi \in \mathit{\Pi}(\mu,\nu), \, (X,Y)\sim\pi}{\inf} \mathbb{E}\left[c(X,Y)\right] \] De manière plus compacte, on note : \[ \mathcal{L}_c(\mu,\nu) \stackrel{\text{déf.}}= \underset{\pi \in \mathit{\Pi}(\mu,\nu)}{\inf} \langle c,\,\pi\rangle \]
Le problème se comprend en interprétant \(\mathrm d \pi(x,y)\) comme la proportion de la masse totale déplacée selon le couplage \(\pi\) entre \(x\) et \(y\), dont le coût est \(c(x,y)\). On veut donc bien minimiser le coût total du transport de \(\mu\) à \(\nu\).
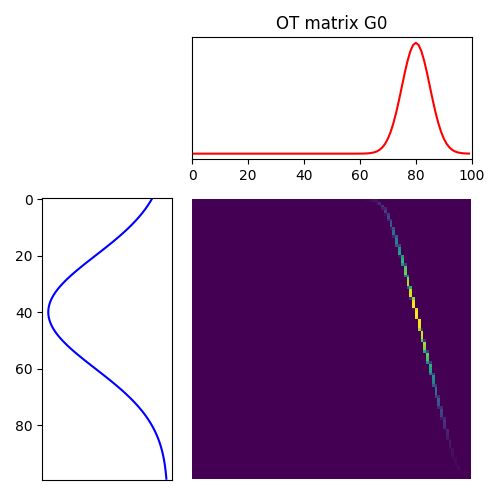
1.1.2 Formulation discrète
Si \(\mathcal{F}=\{x_1,\dots,x_d\}\) est une partie finie de \(\mathcal{X}\), et \(\mu\in\mathop{\mathrm{P}}_f(\mathcal{X})\) est une mesure de probabilité à support fini inclus dans \(\mathcal{F}\), on peut identifier \(\mu\) à son vecteur de probabilité via : \[\begin{array}{rcl} \mathop{\mathrm{P}}_f(\mathcal{X}) & \longrightarrow &\ \Sigma_d=\{ \,{}^t{(\mathrm{\textbf{a}}_1,\dots,\mathrm{\textbf{a}}_d)}\in\mathbb{R}^d, \sum_{i=1}^{i=d} \mathrm{\textbf{a}}_i = 1\} \\ \mu & \longmapsto & \left(\mu(\{x_i\})\right)_{1\leq i\leq d} \\ \end{array}\]
Cette remarque est fondamentale car elle permet d’identifier le problème de Monge-Kantorovitch au problème d’optimisation linéaire (i.e. de minimisation d’une forme linéaire sur un polytope convexe en dimension finie) suivant : \[ \mathrm{L}_{\mathrm{\textbf{C}}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) \stackrel{\text{déf.}}= \underset{\mathrm{\textbf{P}} \in \mathrm{\textbf{U}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})}{\min} \langle \mathrm{\textbf{C}},\,\mathrm{\textbf{P}}\rangle \] où \(\mathrm{\textbf{a}}\in\Sigma_n\), \(\mathrm{\textbf{b}}\in\Sigma_m\), \(\mathrm{\textbf{C}}\in\mathcal{M}_{n,m}(\mathbb{R})\) et : \[ \mathrm{\textbf{U}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) \stackrel{\text{déf.}}= \left\{ \mathrm{\textbf{P}}\in \mathcal{M}_{n,m}(\mathbb{R}_+) : \mathrm{\textbf{P}}\mathbb{1}_m = \mathrm{\textbf{a}}\text{ et } \,{}^t{\mathrm{\textbf{P}}} \mathbb{1}_n = \mathrm{\textbf{b}} \right\} \]
Remarque 1.2. Cette traduction du problème dans sa version discrète est principalement introduite en raison de sa forme matricielle qui se prête bien aux méthodes d’optimisation linéaire de la Section 1.2 et aux algorithmes de résolution qui seront présentés au Chapitre 2.
1.1.3 Existence des solutions
Proposition 1.1 (Existence des solutions) Le problème de Monge-Kantorovitch admet des solutions, i.e. il existe au moins un couplage optimal \(\pi^*\) dans \(\mathit{\Pi}(\mu,\nu)\) tel que : \[\mathcal{L}_c(\mu,\nu)=\int_{\mathcal{X}\times \mathcal{Y}} c(x,y) \, \mathrm{d}\pi^*(x,y) \]
Preuve. Dans le cas où \(\mu\) et \(\nu\) sont à support fini, on se ramène à prouver l’existence d’une solution au problème discret introduit à la Section 1.1.2. Or l’application : \[\begin{array}{rcl} \mathrm{\textbf{U}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) & \longrightarrow &\ \mathbb{R} \\ P & \longmapsto & \langle C,\,P\rangle \\ \end{array}\] est linéaire donc continue et \(\mathrm{\textbf{U}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})\) est un fermé (comme intersection de \(nm\) demi-espaces fermés et de \(n+m\) hyperplans affines), borné (pour la norme d’opérateur par exemple) donc compact; elle atteint donc son minimum en un point \(\mathrm{\textbf{P}}^*\) de \(\mathrm{\textbf{U}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})\).
1.2 Dualité lagrangienne
Le déroulement naturel est alors d’introduire le lagrangien, afin de libérer les contraintes affines :
Définition 1.2 Le lagrangien \(\Lambda_\mathrm{\textbf{C}}\) associé au problème \(\mathrm{L}_\mathrm{\textbf{C}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})\) est défini pour \(\mathrm{\textbf{P}}\in\mathcal{M}(\mathbb{R}_+)\) et \((\mathrm{\textbf{f}},\mathrm{\textbf{g}})\in\mathbb{R}^m\times\mathbb{R}^n\) par : \[\Lambda_\mathrm{\textbf{C}}(\mathrm{\textbf{P}},\mathrm{\textbf{f}},\mathrm{\textbf{g}}) = \langle \mathrm{\textbf{C}},\,\mathrm{\textbf{P}}\rangle + \langle \mathrm{\textbf{a}}-\mathrm{\textbf{P}}\mathbb{1}_m,\,\mathrm{\textbf{f}}\rangle + \langle \mathrm{\textbf{b}}- \,{}^t{\mathrm{\textbf{P}}}\mathbb{1}_n,\,\mathrm{\textbf{g}}\rangle\]
Alors on peut réécrire le problème discret sous la forme : \[\mathrm{L}_\mathrm{\textbf{C}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})=\underset{\mathrm{\textbf{P}}\in\mathcal{M}_{n,m}(\mathbb{R}_+)}{\min}\;\left(\underset{(\mathrm{\textbf{f}},\mathrm{\textbf{g}})\in\mathbb{R}^m\times\mathbb{R}^n}{\max}\;\Lambda_\mathrm{\textbf{C}}(\mathrm{\textbf{P}},\mathrm{\textbf{f}},\mathrm{\textbf{g}})\right)\]
Le problème dual apparaît lors de l’inversion entre \(\min\) et \(\max\) : \[\begin{aligned} \widehat{\mathrm{L}}_\mathrm{\textbf{C}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}}) & \stackrel{\text{déf.}}= \underset{(\mathrm{\textbf{f}},\mathrm{\textbf{g}})\in\mathbb{R}^m\times\mathbb{R}^n}{\max}\;\left(\underset{\mathrm{\textbf{P}}\in\mathcal{M}_{n,m}(\mathbb{R}_+)}{\min}\;\Lambda_\mathrm{\textbf{C}}(\mathrm{\textbf{P}},\mathrm{\textbf{f}},\mathrm{\textbf{g}})\right) \\ & = \underset{(\mathrm{\textbf{f}},\mathrm{\textbf{g}})\in\mathbb{R}^m\times\mathbb{R}^n}{\max}\; \langle \mathrm{\textbf{f}},\,\mathrm{\textbf{a}}\rangle+\langle \mathrm{\textbf{g}},\,\mathrm{\textbf{b}}\rangle + \underset{\mathrm{\textbf{P}}\in\mathcal{M}_{n,m}(\mathbb{R}_+)}{\min}\; \langle \mathrm{\textbf{C}}- \mathrm{\textbf{f}}\, \,{}^t{\mathbb{1}_m}- \mathbb{1}_n \,{}^t{\mathrm{\textbf{g}}},\,\mathrm{\textbf{P}}\rangle \end{aligned}\]
Or on a : \[\underset{\mathrm{\textbf{P}}\in\mathcal{M}_{n,m}(\mathbb{R}_+)}{\min}\; \langle \mathrm{\textbf{C}}- \mathrm{\textbf{f}}\, \,{}^t{\mathbb{1}_m}- \mathbb{1}_n \,{}^t{\mathrm{\textbf{g}}},\,\mathrm{\textbf{P}}\rangle=\left\{\begin{array}{rl} 0 & \text{ si } \mathrm{\textbf{C}}- \mathrm{\textbf{f}}\, \,{}^t{\mathbb{1}_m} - \mathbb{1}_n \,{}^t{\mathrm{\textbf{g}}}\in\mathcal{M}_{n,m}(\mathbb{R}_+) \\ -\infty & \text{ sinon} \end{array}\right.\]
Ainsi : \[
\widehat{\mathrm{L}}_\mathrm{\textbf{C}}(\mathrm{\textbf{a}},\mathrm{\textbf{b}})=\underset{(\mathrm{\textbf{f}},\mathrm{\textbf{g}})\in\mathrm{\textbf{R}}(\mathrm{\textbf{C}})}{\max}\; \langle \mathrm{\textbf{f}},\,\mathrm{\textbf{a}}\rangle+\langle \mathrm{\textbf{g}},\,\mathrm{\textbf{b}}\rangle
\] où \(\mathrm{\textbf{R}}(\mathrm{\textbf{C}})=\{(\mathrm{\textbf{f}},\mathrm{\textbf{g}})\in\mathbb{R}^n\times\mathbb{R}^m, \forall\,(i,j)\in
[1,m] \times [1,n], \mathrm{\textbf{f}}_i+\mathrm{\textbf{g}}_j\leq \mathrm{\textbf{C}}_{i,j}\}\).
Cette équation peut se réécrire dans le formalisme du problème initial dans le cas où les mesures sont à support fini :
Définition 1.3 (Problème de Monge-Kantorovitch, énoncé dual) \[ \widehat{\mathcal{L}}_c(\mu,\nu)=\underset{f,g\in\mathcal{R}(c)}{\sup}\;\langle f,\,\mu\rangle+\langle g,\,\nu\rangle = \underset{f,g\in\mathcal{R}(c)}{\sup}\; \mathbb{E}_{X\sim\mu}\left[f(X)\right] + \mathbb{E}_{Y\sim\nu}\left[g(Y)\right] \]
Remarque 1.3. La régularité des potentiels \(f\) et \(g\) n’a que peu d’importance dans l’écriture ci-dessus pour des mesures à support fini. En revanche, l’énoncé dual général nécessite une hypothèse de continuité (ou le caractère 1-lipschitzien) des potentiels pour que les résultats ci-dessous puissent se généraliser.
Théorème 1.1 (Dualité faible, dualité forte)
- (Dualité faible). \[\widehat{\mathcal{L}}_c(\mu,\nu)\leq \mathcal{L}_c(\mu,\nu)\]
- (Dualité forte). \[\widehat{\mathcal{L}}_c(\mu,\nu)= \mathcal{L}_c(\mu,\nu)\]
Preuve. On exposera la preuve dans le cas où les mesures sont à support fini. La dualité générale est démontrée par Villani (2009).
(Dualité faible). Celle-ci découle simplement du fait que le plus grand des minima est inférieur au plus petit des maxima.
(Dualité forte). La dualité forte se démontre en suivant l’algorithme du simplexe, ou via le lemme de Farkas, qui se déduit du théorème de séparation point/convexe-fermé par des hyperplans. C’est un résultat général pour tous les problèmes d’optimisation linéaire admettant une solution.