3  Des distances sur les distributions de probabilités

Dans ce chapitre, on supposera que \(\mathcal{X}=\mathcal{Y}\) est un espace métrique muni d’une distance \(d\) et de sa tribu de Borel \(\mathcal{B}(\mathcal{X})\). On va montrer qu’alors la distance \(d\) sur \(\mathcal{X}\) induit, via le transport optimal, une famille de distances sur un sous-espace de \(\mathrm{P}(\mathcal{X})\) contenant les mesures à support fini (et égal à l’espace tout entier si l’on suppose en outre \(\mathcal{X}\) compact).

3.1 La distance de \(p\)-Wasserstein

Définition 3.1 On définit, si \(p\geq 1\), la distance de \(p\)-Wasserstein par : \[\mathcal{W}_p (\mu,\nu) = \left(\mathcal{L}_{d^p} (\mu,\nu)\right)^\frac{1}{p}\in \left[0,+\infty\right]\]

Proposition 3.1 Si \(\mathcal{X}\) est séparable complet, la distance de \(p\)-Wasserstein est une distance sur : \[\mathrm{P}_p (\mathcal{X}) = \{\mu \in \mathrm{P} (\mathcal{X}), \exists\, x_0\in\mathcal{X}, \langle d(x_0,\cdot)^p,\,\mu\rangle<+\infty\}\]

Preuve. Présentons la preuve proposée par Villani (2009). Montrons d’abord que \(\mathcal{W}_p\) vérifie les axiomes d’une distance, nous montrerons ensuite qu’elle est à valeurs réelles sur \(\mathrm{P}_p(\mathcal{X})\).

Soit \(\mu,\nu,\xi\) des mesures de probabilité sur \(\mathcal{X}\).

  1. (Symétrie). Elle découle de celle du problème de Monge-Kantorovitch.

  2. (Séparation). Notons \(\pi\in\mathit{\Pi}(\mu,\mu)\) le couplage défini par : \[\pi(A\times B)=\mu(A\cap B) \text{ si } A,B\in\mathcal{B}(\mathcal{X})\] de sorte que si \((X,Y)\sim\pi\), on a \(X=Y \text{ p.s.}\) d’où \(\mathbb{E}[d(X,Y)]=0\) et \(\pi\) est optimal : \(\mathcal{W}_1(\mu,\mu)=0\). Réciproquement, si \(\mathcal{W}_p(\mu,\nu)=0\), soit \((X,Y)\) un couplage optimal de \((\mu,\nu)\) (dont l’existence est garantie par la Proposition 1.1). Alors \(d(X,Y)=0\) p.s., i.e. \(X=Y\) p.s. (par séparation de \(d\)), et en particulier \(X\sim Y\). D’où \(\mu=\nu\).

  3. (Inégalité triangulaire). Commençons par fixer un couplage optimal \((X,Y)\) (et \((Y,Z\))) de \((\mu,\nu)\) (respectivement \((\nu,\xi)\)), on utilise ensuite le lemme gluant, prouvé par Villani (2003) :

    Lemme 3.1 (gluant) Soit \(\mathcal{X}_1\), \(\mathcal{X}_2\), \(\mathcal{X}_3\) des espaces polonais (métriques, complets, séparables), et \(\mu_1\), \(\mu_2\), \(\mu_3\) des mesures de probabilité sur ces espaces respectifs. Si \(\pi_{12}\in\mathit{\Pi}(\mu_1,\mu_2)\) et \(\pi_{23}\in\mathit{\Pi}(\mu_2,\mu_3)\) sont deux couplages, alors il existe une mesure de probabilité \(\pi\in\mathrm{P}(\mathcal{X}_1\times\mathcal{X}_2\times\mathcal{X}_3)\) ayant pour marges \(\pi_{12}\) sur \(\mathcal{X}_1\times\mathcal{X}_2\) et \(\pi_{23}\) sur \(\mathcal{X}_2\times\mathcal{X}_3\).

    Par le lemme, on dispose d’un triplet \((X',Y',Z')\in\mathrm{P}(\mathcal{X}^3)\) tel que \((X',Y')\) et \((Y',Z')\) soient égales en loi respectivement à \((X,Y)\) et \((Y,Z)\); en particulier, \((X',Z')\) est un couplage de \((\mu,\xi)\). D’où : \[\begin{aligned} \mathcal{W}_p(\mu,\xi) & \leq \mathbb{E}\left[d(X',Z')^p\right]^\frac{1}{p} \\ & \leq \mathbb{E}\left[(d(X',Y')+d(Y',Z'))^p\right]^\frac{1}{p} \text{ (inégalité triangulaire)} \\ & \leq \left(\mathbb{E}\left[d(X',Y')^p\right] + \mathbb{E}\left[d(Y',Z')^p\right]\right)^\frac{1}{p} \text { (inégalité de Minkovski)} \\ \mathcal{W}_p(\mu,\xi) & \leq \mathcal{W}_p(\mu,\nu) + \mathcal{W}_p(\nu,\xi) \end{aligned}\] C’est l’inégalité triangulaire attendue.

Enfin, montrons que \(\mathcal{W}_p\) prend des valeurs finies sur \(\mathrm{P}_p(\mathcal{X})\). Si \(\mu\) et \(\nu\) sont dans \(\mathrm{\textbf{P}}_p(\mathcal{X})\), et \(\pi\in\mathit{\Pi}(\mu,\nu)\), alors l’inégalité (découlant par exemple du binôme de Newton) : \[d(x,y)\leq 2^{p-1} (d(x,x_0)^p+d(x_0,y)^p)\] montre qu’il suffit que \(d(\cdot,x_0)^p\) soit \(\mu\)-intégrable et \(d(x_0,\cdot)^p\) soit \(\nu\)-intégrable pour que \(d^p\) soit \(\pi\)-intégrable, et de plus que la définition de \(\mathrm{P}_p(\mathcal{X})\) ne dépend pas du choix de \(x_0\in\mathcal{X}\). 

Exemple 3.1 On a immédiatement que la distance de \(p\)-Wasserstein entre deux mesures de Dirac est donnée par : \[\mathcal{W}_p(\delta_x,\delta_y)=d(x,y) \text{ si } (x,y)\in\mathcal{X}^2\]

3.2 Les autres distances et divergences classiques

L’idée de quantifier la dissimilarité entre deux distributions n’est pas nouvelle, et de nombreuses divergences ont été étudiées, notamment la divergence de Kullback-Leibler, qui s’interprète comme l’entropie relative des deux distributions.

Définition 3.2 Une divergence sur un ensemble \(\mathcal{E}\) est une application \(d\) de \(\mathcal{E}^2\) dans \(\mathbb{R}_+\) séparant les points : \[\forall (x,y)\in\mathcal{E}^2, x=y \iff d(x,y)=0\]

  1. (Distance en variation totale). \[\delta(\mu,\nu)=\underset{A\in\mathcal{B}(\mathcal{X})}{\sup}\;\left|\mu(A)-\nu(A)\right|\]
  2. (Divergence de Kullback-Leibler). \[\mathop{\mathrm{KL}}(\mu,\nu)=\int_{\mathcal{X}}\log\left(\frac{\mu(x)}{\nu(x)}\right)\mu(x)\,\mathrm{d}\rho(x)\] où \(\mu\) et \(\nu\) sont absolument continues par rapport à une mesure \(\rho\in\mathrm{P}(\mathcal{X})\).
  3. (Divergence de Jensen-Shannon). \[\mathop{\mathrm{JS}}(\mu,\nu)=\mathop{\mathrm{KL}}(\mu,\xi)+\mathop{\mathrm{KL}}(\nu,\xi) \text{ où } \xi=\frac{\mu+\nu}{2}\]

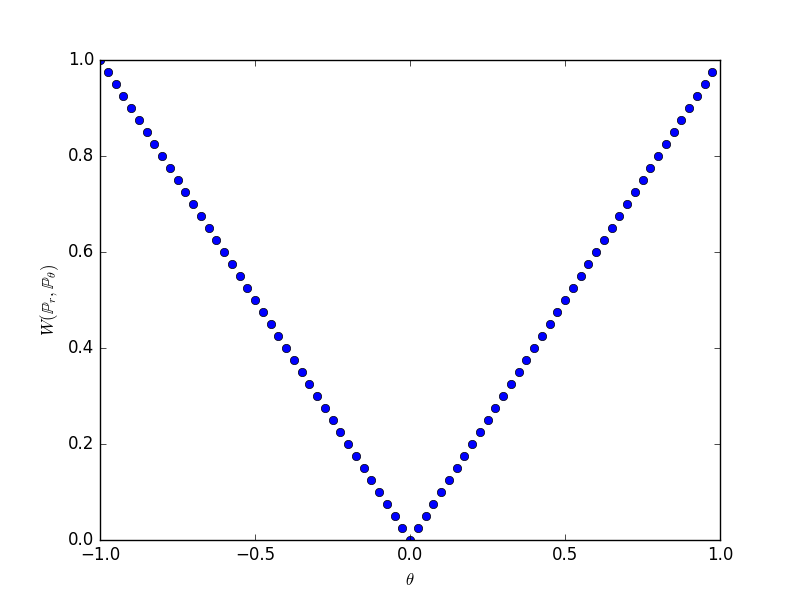
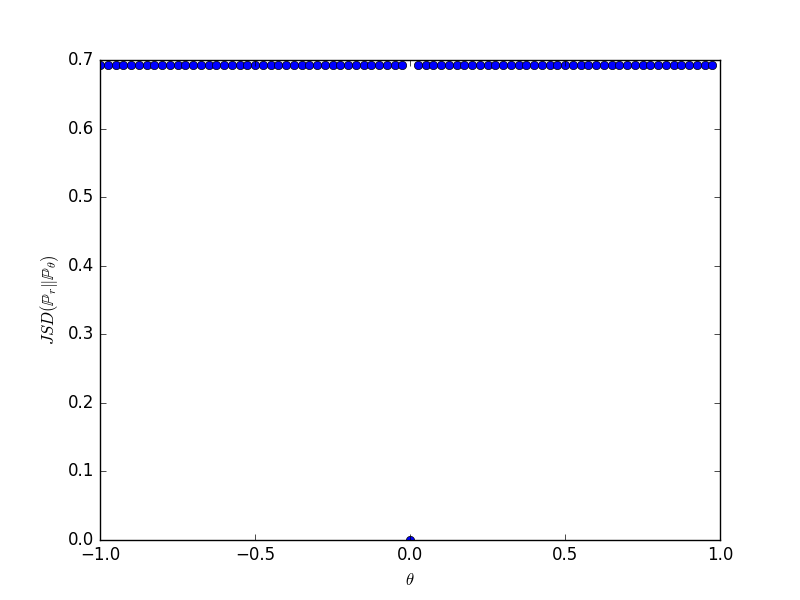
Exemple 3.2 Prenons \(\mathcal{X}=\mathbb{R}^2\) et \(Y\sim\mathcal{U}([0,1])\). Considérons la famille de mesures de probabilité \((\mu_\theta)_{\theta\in\mathbb{R}}\) où \(\mu_\theta\) est la loi de la variable aléatoire \((\theta,Y)\) (i.e. la distribution uniforme sur le segment vertical d’abscisse \(\theta\)). Alors on a :

  • \(\mathcal{W}_1(\mu_\theta,\mu_0)=\left|\theta\right|\)
  • \(\delta(\mu_\theta,\mu_0)=\delta_{\theta}\) (symbole de Kronecker)
  • \(\mathop{\mathrm{KL}}(\mu_\theta,\mu_0)=+\infty\times\delta_{\theta}\)
  • \(\mathop{\mathrm{JS}}(\mu_\theta,\mu_0=\log 2 \times \delta_{\theta}\)

Figure 3.1: Tracés de \(\mathcal{W}_1(\mu_\theta,\mu_0)\) (à gauche) et \(\operatorname{JS}(\mu_\theta,\mu_0)\) (à droite) en fonction de \(\theta\), illustrant la différence de régularité et de finesse de convergence entre la distance de Wasserstein et la divergence de Jensen-Shannon.

3.3 Comparaison des notions de convergence

Le résultat suivant a été démontré par Arjovsky, Chintala, et Bottou (2017) afin de comparer les notions de convergence induites par les différentes distances et divergences :

Théorème 3.1 Supposons que \(\mathcal{X}\) soit compact. Soit \(\mu\) et \((\mu_n)_{n\in\mathbb{N}}\) dans \(\mathrm{P}(\mathcal{X})\). Alors :

  1. \(\mathop{\mathrm{KL}}(\mu_n,\mu)\rightarrow 0 \text{ ou } \mathop{\mathrm{KL}}(\mu,\mu_n)\rightarrow 0 \implies \delta(\mu_n,\mu)\rightarrow 0\)
  2. \(\delta(\mu_n,\mu)\rightarrow 0 \iff \mathop{\mathrm{JS}}(\mu_n,\mu)\rightarrow 0\)
  3. \(\delta(\mu_n,\mu)\implies \mathcal{W}_1(\mu_n,\mu)\rightarrow 0\)
  4. \(\mathcal{W}_1(\mu_n,\mu)\rightarrow 0\) si, et seulement, si \(\mu_n\) converge étroitement vers \(\mu\).

Preuve.

  1. Le premier résultat découle de l’inégalité de Pinsker : \[\delta(\mu_n,\mu)\leq \sqrt{\frac{1}{2}\mathop{\mathrm{KL}}(\mu_n,\mu)}\rightarrow 0 \text{ et } \delta(\mu,\mu_n)\leq \sqrt{\frac{1}{2}\mathop{\mathrm{KL}}(\mu,\mu_n)}\rightarrow 0\]
  2. Ce résultat est admis, la preuve (calculatoire) est à retrouver en annexe de (Arjovsky, Chintala, et Bottou 2017).
  3. La démonstration est celle de Villani (2009).
  4. Par le théorème de représentation de Riesz, \((\mathrm{P}(\mathcal{X}),\delta)\) est isométrique à une sous-partie de l’espace dual des fonctions continues sur \(\mathcal{X}\). Sa topologie est donc plus fine que la topologie faible \(\star\), d’où le résultat. Villani montre une majoration explicite : \[\mathcal{W}_1(\mu,\nu) \leq \operatorname{Diam} (\mathcal{X}) \, \delta(\mu,\nu)\]